Electricity
Electric circuit
👉 A continuous and closed path of an electric current is called an electric circuit.
 |
| Electric circuit |
Electric Current
👉The amount of charge flowing through a particular area in unit time. In other words, it is the rate of flow of electric charges.
If a net charge `Q`, flows across any cross-section of a conductor in time `t`, then the current `I`, through the cross-section is
`I = \frac{Q}{t}`
I = ne / t (∵ Q = ne)
The SI unit of electric charge is coulomb (C)
The electric current is expressed by a unit called ampere (A)
`1C = 6 × 10^18` electrons.
One ampere
One ampere is constituted by the flow of one coulomb of charge per second, that is,
`1 A = \frac{1 C}{1 s}`.
Small quantities of current are expressed in milliampere (`1 mA = 10^{–3} A`) or in microampere (`1 μA = 10^{–6} A`).
Electric Potential Difference
➤We define the electric potential difference between two points in an electric circuit carrying some current as the work done to move a unit charge from one point B to the other point A.
Potential difference (V) between two points A and B = Work done (W)/Charge (Q).
We express this mathematically as
`V = V_A - V_B = \frac{W}{Q}`
➤The SI unit of electric potential difference is volt (V).
One volt
➤One volt is the potential difference between two points in a current-carrying conductor when 1 joule of work is done to move a charge of 1 coulomb from one point to the other.
1 volt = 1 joule / 1 coulomb
`1 V = 1J C^{-1}`
Q. How much work will be done in bringing a charge of `5.0 mC` from infinity to a point at which the potential is `12V`?
Sol:
The potential at infinity is usually taken as zero. So, the work done is
`W = QV`
`= 5.0 × 10^{-3} C × 12V`
`= 0.06 J`
Q. A particle with a charge of `1.5 C` is taken from point `A` at a potential of `50 V` to another point `B` at a potential of `120 V`. Calculate the work done.
Sol:
`V_A = 50 V`
`V_B = 120V`
`W = Q(V_B - V_A)`
`= 1.5 C × (120 V - 50 V) = 105 J`
OHM’S LAW
➤ Relationship between potential diffrence, `V` and current, `I`.
➤The potential difference, `V`, across the ends of a given metallic wire in an electric circuit is directly proportional to the current flowing through it, provided its temperature remains the same. This is called Ohm’s law.
In other words –
`V \propto I`
or `\frac{V}{I}` = constant = `R`
or `V = IR`
(V–I graph for a nichrome wire. A
straight line plot shows that as the
current through a wire increases, the
potential difference across the wire
increases linearly – this is Ohm’s law.)
 |
| Source: NCERT |
Slope `= \frac{QM}{MP} = \frac{V_2 - V_1}{I_2 - I_1}`
`R` is a constant for the given metallic wire at a given temperature and is called its resistance. It is the property of a conductor to resist the flow of charges through it. Its SI unit is ohm, represented by the Greek letter `\Omega`. According to Ohm’s law,
`R = V/I`
➤ If the potential difference across the two ends of a conductor is `1 V` and the current through it is `1 A`, then the resistance R, of the conductor is 1 `\Omega`.
That is, 1 ohm = 1volt / 1 ampere
On What Does Resistance Depend?
- Resistance depends on the material.
- Resistance depends on the area of the cross-section.
- Resistance depends on the length.
1) Resistance depends on the material
➤ Connect a circuit as shown in the Fig, in which AB represents a wire.
➤ Take wire of different materials, but of the same cross-sectional area (same thickness) and the same length. You may take a nichrome wire, copper wire, and so on.
➤ Connect each wire one by one between A and B. After connecting a particular wire, insert the key into the plug. Then read the ammeter to note the current (I) passing through the wire. You will find that the value of the current is different for different wires. This means that the resistance of a wire of a given length and cross-section area depends on the material of the wire.
2) Resistance depends on the area of cross-section
➤ Repeat the above experiments with wires of the same material and same length, but of different cross-sectional areas. You will find the thicker the wire, greater the current. Resistance is inversely proportional to the area of cross-section (A).
`R \propto \frac{1}{A}`
3) Resistance depends on the length
You will find that when the length is doubled, the current is halved. In other words, the resistance is doubled. And, when the length becomes three times, the resistance also increases three times. Thus resistance is proportional to length.
`R \propto l`
Resistivity
For a given material, resistance is `R \propto \frac{1}{A}` and `R \propto l` . Combing this two
`R \propto \frac{l}{A}`
`R = \rho \frac{l}{A}`
Here, `\rho` is a constant for a given material at a given temperature. It is called the resistivity of the material. The resistivity of a material is the resistance per unit length of a unit cross-section of the material. The SI unit of the resistivity is ohm metre (`\Omega m`).
RESISTANCE OF A SYSTEM OF RESISTORS
➤ The current through a conductor depends upon its resistance and the potential difference across its ends.
In various electrical gadgets, we often use resistors in various combinations. We now, therefore, intend to see how Ohm’s law can be applied to combinations of resistors.
There are two methods of joining the resistors together.
- Resistors connected in series
- Resistors connected in parallel
1. Resistors connected in series
 |
| Resistors in series |
The figure shows an electric circuit in which three resistors having resistances `R_1`, `R_2` and `R_3`, respectively, are joined end to end. Here the resistors are said to be connected in series.
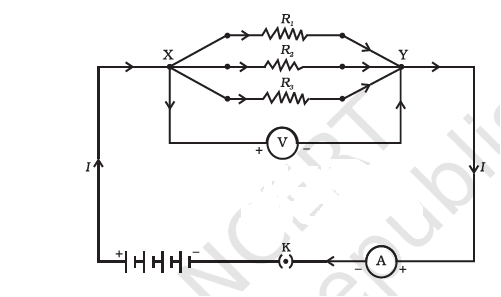
2. Resistors connected in parallel
The figure shows a combination of resistors in which three resistors are connected together between points X and Y. Here, the resistors are said to be connected in parallel.
What happens to the value of current when a number of resistors are connected in series in a circuit? What would be their equivalent resistance?
Let us try to understand these with the help of the following activities.
Activity 1
➠ Join three resistors of different values in the series. Connect them with a battery, an ammeter, and a plug key. You may use the resistors of values like `1 \Omega, 2 \Omega, 3 \Omega`, etc., and a battery of `6 V` for performing this Activity.
➠ Plug the key. Note the ammeter reading.
➠ Change the position of the ammeter to anywhere in between the resistors. Note the ammeter reading each time.
➠ Do you find any change in the value of current through the ammeter?
Conclusion: You will observe that the value of the current in the ammeter is the same, independent of its position in the electric circuit. It means that in a series combination of resistors the current is the same in every part of the circuit or the same current through each resistor.
Activity 2
➠ In Activity, insert a voltmeter across the ends X and Y of the series combination of three resistors.
➠ Plug the key in the circuit and note the voltmeter reading. It gives the potential difference across the series combination of resistors. Let it be `V`. Now measure the potential difference across the two terminals of the battery. Compare the two values.
➠ Take out the plug key and disconnect the voltmeter. Now insert the voltmeter across the ends X and P of the first resistor.
➠ Plug the key and measure the potential difference across the first resistor. Let it be `V_1`.
➠ Similarly, measure the potential difference across the other two resistors, separately. Let these values be `V_2` and `V_3`, respectively.
➠ Deduce a relationship between `V, V_1, V_2`, and `V_3`.
Conclusion: You will observe that the potential difference `V` is equal to the sum of potential differences `V_1, V_2, and V_3`. That is the total potential difference across a combination of resistors in series is equal to the sum of potential difference across the individual resistors. That is,
`V = V_1 + V_2 + V_3`
Let `I` be the current through the circuit. The current through each resistor is also `I`. It is possible to replace the three resistors joined in series by an equivalent single resistor of resistance `R`, such that the potential difference `V` across it, and the current `I` through the circuit remains the same. Applying the Ohm’s law to the entire circuit, we have
`V = I R`
On applying Ohm’s law to the three resistors separately, we further have
`V_1 = I R_1`
`V_2 = I R_2`
`V_3 = I R_3`
`V = V_1 + V_2 + V_3`
`I R = I R_1 + I R_2 + I R_3`
`R_s = R_1 +R_2 + R_3`
We can conclude that when several resistors are joined in series, the resistance of the combination `R_s` equals the sum of their individual resistances, `R_1, R_2, R_3`, and is thus greater than any individual resistance
Heating effect of electric current
Let the potential difference be `V`, current `I` is flowing through the resistor of resistance `R`, and time `t`.
Work done in moving charge `Q`
`W = VQ \because V = W/Q`
Work done per unit time is power
`W/t` = `\frac{VQ}{t}`
`P = \frac{VQ}{t}`
`P = VI \because I = Q/t`
The energy is supplied continuously in time `t`
`P × t = VIt`
Energy get dissipated as heat
`H = VIt`
Applying Ohm's law
`H = (IR)It \because V= IR`
`H = I^2 RT`
This is known as Joule's law of heating.
Or, `H = (V/R)^2 Rt` `\because I = V/R`
`H = V^2/R t`
Joule's law of heating law implies that heat produced in a resistor is
- `H \propto I^2`
- `H \propto R`
- `H \propto t`
Electric Power
The rate of doing work is power. This is also the rate of consumption of energy.
`P = W/t`
`P = \frac{VQ}{t} \because W = VQ`
`P = VI \because I = Q/t`
`P = I^2R \because V = IR`
`P = V^2/R \because I = V/R`
➤ The SI unit of electric power is watt (W). It is the power consumed by a device that carries 1 A of current when operated at a potential difference of 1 V. Thus,
1 W = 1 volt × 1 ampere = 1 V A
➤ Electrical energy is the product of power and time
`P × t = W/t × t = W`
Or, `P × t = VIt`
`W = VIt`
The unit of electric energy is, therefore, watt-hour (W h). One watt-hour is the energy consumed when 1 watt of power is used for 1 hour. The commercial unit of electric energy is a kilowatt-hour (kW h), commonly known as ‘unit’.
1 kW h = 1000 watt × 3600 second
= `3.6 × 10^6` watt second
= `3.6 × 10^6` joule (J)
Electricity Class 10
Mathematical Equations
Q = ne
`I = Q/t` Or, `I = frac{\triangle Q}{ \triangle t}` Or, I = ne/t
`V = W/Q`
`V/I = R` Or, `V = IR`
`R = \rho l/A`
`R_s = R_1 + R_2 + ..... + R_{n-1} + R_n` Or, `\sum_{s = 1}^{n} \R_s`
`1/R_p = 1/R_1 + 1/R_2 + ....+ 1/R_{n-1} + 1/R_n` Or, `\sum_{p = 1}^{n} \1/R_p`
`H = VIt`
`H = I^2 Rt`
`H = V^2/Rt`
`P = W/t`
`P = VI`
`P = I^2R`
`P = V^2/R`
References
- NCERT Science Class 10




This comment has been removed by the author.
ReplyDeleteNice note
ReplyDeleteThank you
DeleteBest notes sir you are super
ReplyDeleteVery important notes 📝thank you so much sir for providing 🙏
ReplyDeleteMast
ReplyDeleteSuper explanation sir
ReplyDeleteThank you
Delete