📝 Matrices
Let us now suppose that we wish to express the information of possession of notebooks and pens by
Radha and her two friends Fauzia and Simran which arranged in the tabular form.
Tabular form
⬇
An arrangement or display of the above kind is called a matrix.
Definition: An ordered rectangular array of numbers or functions in the form of `m` horizontal lines (rows) and `n` vertical lines (columns) is called a matrix of order `m` by `n`, written as `m × n` matrix. The numbers or functions are
called the elements or the entries of the matrix.
We denote matrices by capital letters.
Examples
In the above examples,
the horizontal lines of elements are said to constitute,
rows of the matrix, and the
vertical lines of elements are said to constitute,
columns of the matrix.
Thus A has 3 rows and 2 columns, B has 3 rows and 3 columns.
Order of a matrix
A matrix having `m` rows and `n` columns is called a matrix of order `m × n` or simply m × n matrix (read as an m by n matrix).
So referring to the above examples of matrices, we have
A as 3 × 2 matrix, B as 3 × 3 matrix. We observe that A has 3 × 2 = 6
elements, B has 9 elements.
In general, an `m × n` matrix has the following
rectangular array:
A = `[a_{ij}]_{m×n}` `1\leq i \leq m,
1\leq j \leq n` `i,j \in ℕ`
An element occurring in the ith row and jth column of matrix A will be called the (ij)th element of A, to be denoted by `a_{ij}`
Operations on Matrices
1) Addition of matrices
2) Multiplication of a matrix by a scalar
3) Difference of matrices
4) Multiplication of matrices.
1) Addition of matrices
If `A = [a_{ij}]` and `B = [b_{ij}]` are two matrices of the same order, say `m × n`. Then, the sum of the two matrices `A` and ` B` is defined as a matrix `C = [c_{ij}]_{m × n}`
where `c_{ij} = a_{ij} + b_{ij}, forall i, j`.
2) Multiplication of a matrix by a scalar
If `A = [a_{ij}]_{m × n}` is a matrix and `k` is a scalar, then `kA` is another matrix which is obtained by multiplying each element of `A` by the scalar `k`.
Or,
`kA = k[a_{ij}]_{m × n} = [k (a_{ij})]_{m × n}` that is, `(i, j)^{th}` element of `kA` is `ka_{ij} forall i, j`.
3) Difference of matrices
If `A = [a_{ij}], B = [b_{ij}]` are two matrices of the same order, say `m × n`, then difference `A – B` is defined as a matrix `D = [d_{ij}]`, where `d_{ij} = a_{ij} – b_{ij}, forall i, j`.
Or,
`D = A – B = A + (–1) B`, that is sum of the matrix `A` and the matrix `– B`
Work in progress
References
- NCERT Mathematics Class 12



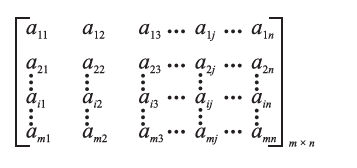
🤗👍👍👍👍👍👍👌👌👌👌👌👌👌👌
ReplyDelete