📝 Vector Algebra
Some Basic Concepts
Scalars A quantity that has magnitude only is known as a scalar.
Examples
Mass, length, speed, time, temperature, density, etc.
Vectors A quantity that has magnitude as well as direction is called a vector.
Examples
Force, velocity, acceleration, etc.
Let `‘l’` be any straight line in-plane or three-dimensional space. This line can be given two directions by means of arrowheads. A line with one of these directions prescribed is called a directed line
Now observe that if we restrict line `l` to the line segment AB, then a magnitude is prescribed on the line `l` with one of the two directions, so that we obtain a directed line segment (Fig iii ). Thus, a directed line segment has magnitude as well as direction.
➤ A quantity that has magnitude, as well as direction, is called a vector.
Notice that a directed line segment is a vector (Fig iii), denoted as `\vec{AB}` or simply as `\vec {a}`, and read as ‘vector `\vec{AB}` ’ or 'vector `\vec {a}`'.
Point A from where the vector `\vec{AB}` starts is called its initial point, and point B where it ends is called its terminal point. The distance between the initial and terminal points of a vector is called the magnitude (or length) of the vector, denoted as | `\vec{AB}` |, or | `\vec {a}` |, or a. The arrow indicates the direction of the vector.
Types of Vectors
Zero Vector A vector whose initial and terminal points coincide, is called a zero vector
(or null vector), and denoted as. A zero vector can not be assigned a definite direction
as it has zero magnitude.
The vectors `\vec (A A)` represent the zero vector
Unit Vector A vector whose magnitude is unity (i.e., 1 unit) is called a unit vector. The
unit vector in the direction of a given vector is denoted by `\hat a`.
`\hat a = frac {\vec a}{|\vec a |}`
Coinitial Vectors Two or more vectors having the same initial point are called coinitial
vectors
Collinear Vectors Two or more vectors are said to be collinear if they are parallel to
the same line, irrespective of their magnitudes and directions.
Equal Vectors Two vectors `\vec a` and `\vec b` are said to be equal, if they have the same
magnitude and direction regardless of the positions of their initial points, and written
as `\vec a = \vec b`
Negative of a Vector A vector whose magnitude is the same as that of a given vector
(say, `\vec {A B}`), but direction is opposite to that of it, is called negative of the given vector.
For example, vector `\vec {BA}` is negative of the vector `\vec {AB}`.
Position Vector
Fig (i), consider a point `P` in space, having coordinates `(x, y, z)` with
respect to the origin `O (0, 0, 0).` Then, the vector `\vec{OP}` having `O` and `P` as its initial and
terminal points, respectively, is called the position vector of the point `P` with respect
to `O. `
The magnitude of `\vec{OP} ( \vec{r})`
`|\vec{OP}| = sqrt{x^2 + y^2 + z^2}`
Fig (ii), in practice, the position vectors of points `A, B, C,` etc., with respect to the origin `O` are denoted by `\vec a , \vec b, \vec c`
Components of a Vector
Let `O` be the origin and let `P( x, y, z)` be any point in space. Let `\hat i, \hat j, \hat k` be the unit vectors along the `x `-axis, `y`-axis and `z`- axis respectively.
Let the position vector `\vec {OP}` be `\vec r`.
Then,
`\vec r = (x \hat i +y \hat j + z \hat k)`
This form of the vector is called its component form.
Here, `x, y, z` are called the scalar components of `\vecr` and `x \hat i, y \hat j, z \hat k` are called its vector components.
Magnitude of `\vec r`
`|\vec r| = | x \hat i + y \hat j + z \hat k | = sqrt{x^2 + y^2 + z^2}`
Direction Ratios & Direction Cosines of a Vector
Let a vector `\vec r = a \hat i + b \hat j +c \hat k`
Then, number `a,b,c` are called the direction ratios of `\vec r`
Direction cosines of `\vec r` are:
`frac{a}{\sqrt{a^2 +b^2 + c^2}}, frac{b}{\sqrt{a^2 +b^2 + c^2}}` and `frac{c}{\sqrt{a^2 +b^2 + c^2}}`
👉 Direction cosines of the vector `\vec r` , are usually denoted by `l, m` and `n`,
respectively.
👉 The magnitude `r`, direction ratios `(a, b, c)` and direction cosines `(l, m, n)` of any
vector are related as:
` l = a/r, m = b/r, n = c/r`
👉 `l^2
+ m^2
+ n^2
= 1`
Remarks
👉 Two vectors `\vec a and \vec b` are collinear
`⇔ \vec b = \lambda \vec a, \lamda \ne 0`
👉 If it is given that `l, m, n` are direction cosines of a vector, then `(l \hat i + m \hat j + n \hat k)` is the unit vector in the direction of that vector,.
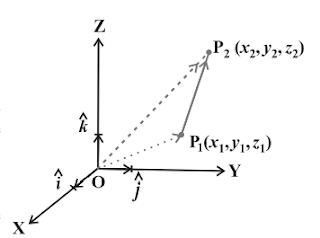
Vector joining two points
If `P_1
(x_1
, y_1
, z_1
)` and `P_2
(x_2
, y_2
, z_2
)` are any two
points, then the vector joining `P_1` and `P_2` is the
vector `vec{P_1 P_2}`
Joining the points `P_1` and `P_2` with the origin `O`, and applying triangle law, from the `\triangle
OP_1
P_2` , we have
`\vec {OP_1} + \vec {P_1P_2} = \vec {OP_2}`
Section formula
The position vector of a point `R` dividing a line segment joining the points `P` and `Q` whose position vectors are `\vec a` and `\vec b` are respectively, in the ratio `m: n`
(i) internally, is given by `\frac {m \vec b +n \vec a}{m +n}`
(ii) externally, is given by `\frac {m \vec b - n \vec a}{m - n}`
Scalar (or dot) product of two vectors
The scalar product of two nonzero vectors, `\vec a` and `\vec b` denoted by `\vec a . \vec b`, is defined as
`\vec a . \vec b = |\vec a| |\vec b| \cos \theta `
where, `\theta` is the angle between `\vec a` and `\vec b`, `0 \leq \theta \leq \pi`
Observations
👉 `\vec a . \vec b` is a real number.
👉 Let `\vec a` and `vec b` be two nonzero vectors, then
`\vec a . \vec b = 0 ⇔ \vec a ⟂ vec b`
👉 If `θ = 0`, then `\vec a . \vec b = |\vec a| |\vec b|`
In particular, `\vec a . \vec a = |\vec a|^2`, as `θ` in this case is `0`.
👉 If either `\vec a = 0` or `\vec b = 0` then `θ` is not defined, and in this case, we
define
`\vec a . \vec b = 0`
👉 For mutually ⟂ unit vectors `\hat i , \hat j` and `\hat k` , we have
`\hat i .\hat i = \hat j .\hat j = \hat k. \hat k = 1`
`\hat i . \hat j = \hat j . hat k = \hat k . hat i = 0`
👉 The angle between two nonzero vectors `\vec a` and `\vec b`
`cos θ = \frac{\vec a . \vec b}{ |\vec a| |\vec b|}`
` ⇒ θ = cos^{-1} (\frac{\vec a . \vec b}{ |\vec a| |\vec b|})`
Cauchy-Schwartz inequality
Prove that `|\vec a · \vec b| ≤ |\vec a||\vec b|`
Proof:
If `\vec a = 0 = \vec b`, then `|\vec a · \vec b| = |\vec a||\vec b|`
Let `\vec a ≠ 0 ≠ \vec b`, then
`\vec a · \vec b = |\vec a||\vec b| \cos \theta`
`⇒ |\vec a · \vec b| = |\vec a||\vec b| |\cos \theta|`
`⇒ \frac{|\vec a · \vec b|}{ |\vec a||\vec b| } = |\cos \theta| ≤ 1`
`⇒ |\vec a · \vec b| ≤ |\vec a||\vec b|`
Hence, `|\vec a · \vec b| ≤ |\vec a||\vec b|`
👉If `\vec a` and `\vec b` represent the adjacent sides of a triangle then its area is given as
`\frac{1}{2}|\vec a \times \vec b|`
`ar(\Delta ABC) = 1/2 AB · CD`
`AB = |\vec b|` and `CD = |\vec a| sin \theta`
Thus, `ar(\Delta ABC) = 1/2 |\vec b| |\vec a| sin \theta = 1/2 |\vec a \times \vec b|`




Good explanation to understand in better way
ReplyDeleteVery nice
ReplyDelete