📝Areas Related to Circles
Multiple Choice Questions + Assertions & Reasons + Case Stidies + Questions
Multiple Choice Questions
1. If the sum of the areas of two circles with radii `R_1` and `R_2` is equal to the area of a circle of radius `R`, then
(A) `R_1 + R_2 = R`
(B) `R_1^2 + R_2^2 = R^2`
(C) `R_1 + R_2 < R`
(D) `R_1^2 + R_2^2 <R^2`
2. If the sum of the circumferences of two circles with radii `R_1` and `R_2` is equal to the circumference of a circle of radius `R`, then
(A) `R_1 + R_2 = R`
(B) `R_1 + R_2 > R`
(C) `R_1 + R_2 < R`
(D) Nothing definite can be said about the relation among `R_1, R_2` and `R`.
3. If the circumference of a circle and the perimeter of a square are equal, then
(A) Area of the circle `=` Area of the square
(B) Area of the circle `>`Area of the square
(C) Area of the circle `<` Area of the square
(D) Nothing definite can be said about the relation between the areas of the circle and square.
4. If the perimeter of a circle is equal to that of a square, then the ratio of their areas is
(A) 22 : 7
(B) 14 : 11
(C) 7 : 22
(D) 11: 14
5. It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be
(A) 10 m
(B) 15 m
(C) 20 m
(D) 24 m
6. Tick the correct answer in the following and justify your choice: If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(A) 2 units
(B) p units
(C) 4 units
(D) 7 units
7. The area of the circle that can be inscribed in a square of side 6 cm is
(A) 36 `\pi cm^2`
(B) 18 `\pi cm^2`
(C) 12 `\pi cm^2`
(D) 9 `\pi cm^2`
8. The area of a circular path of uniform width d surrounding a circular region of radius r is
(A) `\pid ( 2r + d)`
(B) `\pi (2r + d) r`
(C) `\pi (d + r)`
(D) `\pi (d + r) d`
9. If the circumference of a circle increases from `4 \pi` to `8 \pi` , then its area is
(A) halved
(B) doubled
(C) tripled
(D) quadrupled
10. If the radius of a circle is diminished by 10%, then its area is diminished by
(A) 10%
(B) 19%
(C) 36%
(D) 20%
★★★★★★★★
Assertion & Reason
(a) If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
(c) If Assertion is true but Reason is false.
(d) If Assertion is false but Reason is true.
1. Assertion: If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason: Circumference = `2pi ×` radius
2. Assertion: If the outer and inner diameter of a circular path is 10 m and 6 m then the area of the path is `16pi m^2`.
Reason: If R and r be the radius of outer and inner circular path, then the area of the path is `pi (R^2- r^2)`.
3. Assertion: If a wire of length 22 cm is bent in the shape of a circle, then the area of the circle so formed is 40 `cm^2`.
Reason: Circumference of the circle = length of the wire.
★★★★★★★★
Case Studies
CASE STUDY 1:
Pookalam is the flower bed or flower pattern designed during Onam in Kerala. It is similar as Rangoli in North India and Kolam in Tamil Nadu. During the festival of Onam, your school is planning to conduct a Pookalam competition. Your friend who is a partner in the competition, suggests two designs given below. Observe these carefully.
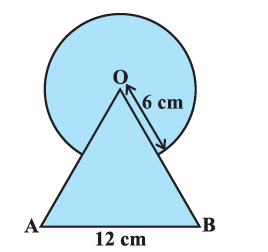
Design I: This design is made with a circle of radius 32cm leaving equilateral triangle ABC in the middle as shown in the given figure.
Design II: This Pookalam is made with 9 circular designs each of radius 7cm.
Refer Design I:
1. The side of an equilateral triangle is
a) 12`\sqrt3` cm
b) 32`\sqrt3` cm
c) 48cm
d) 64cm
2. The altitude of the equilateral triangle is
a) 8 cm
b) 12 cm
c) 48cm
d) 52cm
Refer Design II:
3. The area of the square is
a) 1264 `cm^2`
b) 1764 `cm^2`
c) 1830 `cm^2`
d) 1944 `cm^2`
4. Area of each circular design is
a) 124 `cm^2`
b) 132 `cm^2`
c) 144 `cm^2`
d) 154 `cm^2`
5. Area of the remaining portion of the square ABCD is
a) 378 `cm^2`
b) 260 `cm^2`
c) 340 `cm^2`
d) 278 `cm^2`
ANSWERS:
1. b) 32`\sqrt3` cm
2. c) 48cm
3. b) 1764 `cm^2`
4. d) 154 `cm^2`
5. a) 378 `cm^2`
CASE STUDY 2:
A brooch is a small piece of jewellery which has a pin at the back so it can be fastened on a dress, blouse, or coat. Designs of some brooch are shown below. Observe them carefully.
Design A: Brooch A is made with silver wire in the form of a circle with a diameter of 28mm. The wire is used for making 4 diameters which divides the circle into 8 equal parts.
Design B: Brooch b is made of two colours_ Gold and silver. The outer part is made with Gold. The circumference of the silver part is 44mm and the gold part is 3mm wide everywhere.
Refer to Design A
1. The total length of the silver wire required is
a) 180 mm
b) 200 mm
c) 250 mm
d) 280 mm
2. The area of each sector of the brooch is
a) 44 `mm^2`
b) 52 `mm^2`
c) 77 `mm^2`
d) 68 `mm^2`
Refer to Design B
3. The circumference of the outer part (golden) is
a) 48.49 mm
b) 82.2 mm
c) 72.50 mm
d) 62.86 mm
4. The difference of areas of golden and silver parts is
a) 18 `pi`
b) 44 `pi`
c) 51 `pi`
d) 64 `pi`
5. A boy is playing with brooch B. He makes revolution with it along its edge. How many complete revolutions must it take to cover 80 mm?
a) 2
b) 3
c) 4
d) 5
ANSWERS:
1. b) 200 mm
2. c) 77 `mm^2`
3. d) 62.86 mm
4. c) 51`pi`
5. c) 4
★★★★★★★
Questions
Q. Find the area of a circle whose circumference is 66 cm.
Ans: 346.5 `cm^2`
Q. A steel wire, when bent in the form of a square, encloses an area of 121 `cm^2`. The same wire is bent in the form of a circle. Find the area of the circle.
Ans: 154 `cm^2`
Q. A wire is looped in the form of a circle of radius 28 cm. It is rebent into a square form. Determine the length of the side of the square.
Ans: 44 cm
Q. In covering a distance `s` metres, a circular wheel of radius `r` metres makes `\frac{s}{2\pir}` revolutions. Is this statement true? Why?
Q. A circular park, 42 m in diameter, has a path 3.5 m wide running around it on the outside. Find the cost of gravelling the path at ₹ 20 per `m^2`
Ans: ₹10010
Q. A road that is 7m wide surrounds a circular park whose circumference is 352m. Find the area of the road.
Ans: 2618 `m^2`
Q. A road track is in the form of a ring whose inner and outer circumferences are 437 m and 503 m respectively. Find the width of the track and also its area
Ans: 10.5, 4935 `m^2`
Q. If the perimeter of a semicircular protractor is 36 cm, find its diameter.
Ans: 14 cm
Q. The circumference of a circle exceeds its diameter by 45 cm. Find the circumference of the circle.
Ans: 66 cm
Q. The sum of the radii of two circles is 7cm and the difference of their circumferences is 8 cm. Find the circumferences of the circles.
Q. An archery target has three regions formed by three concentric circles as shown in Fig. If the diameters of the concentric circles are in the ratio 1: 2:3, then find the ratio of the areas of three regions.
Q. The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6: 05 am and 6: 40 am.
Q. Fig. depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Q. The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Q. A bicycle wheel makes `5 × 10^3` revolutions in moving 11 km. Find the diameter of the wheel.
Ans: 70
Q. The diameter of each wheel of a bus is 140 cm. How many revolutions per minute must a wheel make in order to move at a speed of 60 km per hour?
Ans: 250
Q. Two circles touch externally. The sum of their areas is `130\pi cm^2` and the distance between their centres is 14 cm. Find the radii of the circles.
Ans: 11 cm , 3 cm
Q. A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
Q. Prove that the area of a circular path of uniform width `h` surrounding a circular region of radius `r` is `pi h ( 2r + h)`
Q. Find the area of a quadrant of a circle whose circumference is 22 cm.
Ans: `77/8 cm^2`
Q. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Ans: `154/3 cm^2`
Q. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find: (i) the length of the arc (ii) area of the sector formed by the arc (iii) area of the segment formed by the corresponding chord.
Ans: 22 cm, `231 cm^2, (231 - frac{441sqrt3}{4}) cm^2`
Q. A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (i) the area of that part of the field in which the horse can graze. (ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use `pi` = 3.14)
Ans: `19.625 m^2`, `58.875 m^2` Q. A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find : (i) the total length of the silver wire required. (ii) the area of each sector of the brooch.
Ans: 285 mm, `385/4 mm^2`
Ans: `22275/28 cm^2`
Q. A car has two wipers that do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
Ans: `158125/126 cm^2`
Q. To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use `pi` = 3.14).
Ans: 189.97 `km^2`
Q. A round table cover has six equal designs as shown in Fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of ₹0.35 per `cm^2`. (Use `sqrt3` = 1.7)
Ans: ₹162.68
Q. In Fig., two circular flower beds have been shown on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
Ans: 4032 `m^2`Q. Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
Ans: `462 cm^2`
Q. Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
Ans: `frac{25 pi}{4} + 25/2 cm^2`
Q. Find the number of revolutions made by a circular wheel of area `1.54 m^2` in rolling a distance of 176 m.
Ans: 40
Q. Area of a sector of central angle 200° of a circle is `770 cm^2`. Find the length of the corresponding arc of this sector.
Ans: 73 `1/3` cm
Q. The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6: 05 am and 6: 40 am.
Ans: `45 5/6 cm^2`
Q. Area of a sector of a circle of radius 36 cm is `54 pi cm^2`. Find the length of the corresponding arc of the sector.
Ans: `3 pi` cm
Q. With the vertices A, B, and C of a `\triangle` ABC as centres, arcs are drawn with radii 5 cm each as shown in Fig. If AB = 14 cm, BC = 48 cm and CA = 50 cm, then find the area of the shaded region. (Use `pi = 3.14`).
Ans: 296.75 `cm^2`
Q. A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m. If the length of the rope is increased by 5.5m, find the increase in the area of the grassy lawn in which the calf can graze.
Ans: `75.625 m^2`.Q. Find the area of the shaded region in Fig., where ABCD is a square of side 14 cm.
Ans: 42 `cm^2`
Q. Find the area of the shaded region in Fig., if PQ = 24 cm, PR = 7 cm, and O is the centre of the circle.
Ans: `(16pi – 32 ) cm^2`
Q. Find the area of the shaded field shown in Fig.
Ans: `(660/7 + 36sqrt3) cm^2`
Q. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. Find the area of the design.
Ans: `(22528/7 -768sqrt3) cm^2`Q. Fig., depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :
(i) the distance around the track along its inner edge
(ii) the area of the track.
Ans: `2804/7 m, 4320 m^2`
Q. In Fig., AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Ans: `66.5 cm^2`Q. The area of an equilateral triangle ABC is `17320.5 cm^2`. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle. Find the area of the shaded region. (Use `pi = 3.14` and `sqrt3 = 1.73205`)
Ans: `1620.5 cm^2`
Q. In Fig., a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use `pi` = 3.14)
Ans: `228 cm^2`Q. In Fig., ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
Ans: `98 cm^2`
Q. Calculate the area of the designed region in Fig., common between the two quadrants of circles of radius 8 cm each.
Ans: `256/7 cm^2`
Q. Find the area of the shaded region given in Fig.
Q. In Fig., ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.
More questions will be updated soon
References:
- NCERT Mathematics Class X
- R.S. Aggarwal
- NCERT Exemplar
- R.D. Sharma




















👍👍👍👍👍
ReplyDeleteHard question is there plz try all of you
ReplyDeleteGood question🙋🙋
ReplyDelete#cbsc
Very nice sir ✌
ReplyDeleteVery very hard questions and tuesed ☆☆☆☆☆
ReplyDeleteVery good and hard questions
ReplyDeleteThank you
Delete