Introduction to Trigonometry Class 10 | Trigonometry (Notes & Video lectures) | Class 10

Introduction to Trigonometry



Trigonometry 

The word 'trigonometry' is derived from the Greek words 'tri' (meaning three), 'gon' (meaning sides), and 'metron' (meaning measure). Trigonometry is the study of relationships between the sides and angles of a triangle. 
In this chapter, we will study some ratios of the sides of a right triangle with respect to its acute angles, called trigonometric ratios of the angle. We will also define the trigonometric ratios for angles of measure 0° and 90°.


Trigonometric ratios (T- Ratios) of an acute angle of a right-angled triangle

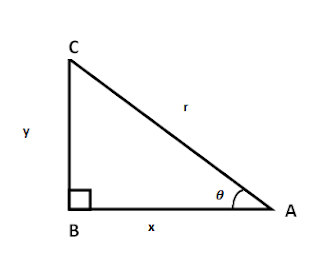
Let `angle BAC = θ` be an acute angle of a right-angled triangle `\triangleABC`.
In right-angled `\triangleABC`, let
base = AB = x units,
perpendicular = BC = y units                                            
and hypotenuse = AC = r units.
Introduction to Trigonometry Class 10, Trigonometry

We define the following ratios, known as Trigonometric Ratios for `θ`
  1. sine `θ` = perpendicular/hypotenuse  = `\frac {BC}{AC}` = `\frac {y} {r}`, and is written as sin `θ`
  2. cosine `θ` = base/hypotenuse =  `frac {AB} {AC)` = `\frac {x} {r}`, and is written as cos `θ` 
  3. tangent `θ` = perpendicular/base = `\frac (BC}{AB}` = `\frac {y} {x}`, and is written as tan `θ`
  4. cosecant `θ` = hypotenuse/perpendicular =  `\frac {AC}{BC}` = `\frac {r} {y}`, and is written as cosec `θ`
  5. secant `θ` = hypotenuse/base =  `\frac {AC}{AB}` = `\frac {r} {x}`, and is written as sec `θ`
  6. cotangent `θ` = base/perpendicular = `\frac {AB}{BC}` =  `\frac {x} {y}`, and is written as cot `θ`
Some people have curly black hair tightly pulled back. 
S → sin `θ`,  c  →  cos `θ`,  t →  tan `θ`

Reciprocal relations 

(i) cosec `θ` =  `1/ sin θ`    (ii) sec `θ` = `1/ cos θ`    (iii)  cot `θ` = `1/ tan θ`

👉 The trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.

Show that the value of each of the trigonometric ratios of an angle does not depend on the size of the triangle. It only depends on the angle. 

Introduction to Trigonometry Class 10, Trigonometry
Proof  Consider a `\triangleABC` in which `\angle B = 90^°`
Take a point `P` on `AC`  and draw  PM ⊥ AB
Then, `\triangleAMP` ~ `\triangleABC`
∴ `\frac {AM}{AB}` =  `\frac {AP}{AC}` = `\frac {PM}{CB}`

⇒ `\frac {PM}{AP}` =  `\frac {CB}{AC}` = `sin A`



Works in progress...







References
  1. Mathematics NCERT Class X
  2. R. S. Aggarwal Mathematics Class X
  3. R. D. Sharma Mathematics Class X


4 Comments